ESTRUCTURA DE DATOS II
TEMAS
- Tipo de dato abstracto arbol
- Formas de recorrer un árbol
- Arboles binarios
- Arboles binarios similares
- Arboles binarios equivalentes
- Arboles tejidos
- Arboles AVL
- Rotacion simple por la derecha
- Rotacion simple por la izquierda
- Doble rotacion por la derecha
- Doble rotacion por la izquierda
- Arboles B
- Arboles B+
- Grafos
- Tipos de grafos
- Grafo dirigido
- Adyacencia
- Incidencia
- Grafo fuertemente conectado
- Grafo debilmente conectado
- Camino simple
- Grafo euleriano
- Grafo Hamiltoniano
- Orden de un grafo
- Grado de un vertice
- Grafos regulares
- Grafo ciclico
- Multigrafo
- Grafo simple
- Grafo completo
- Grafo simetrico
- Lista de adyacencia
- Matriz de adyacencia
- Lista de adyacencia invertida
- Algoritmo de Warshall
- Aplicaciones de grafos
- Algoritmo de Dijsktra
- Algoritmo de Kruskal
- Grafos particulares
- Arboles enearios
- Matrices dispersas
T.D.A Arbol
Un árbol es una colección de elementos, llamados nodos, uno de los cuales se distingue con el nombre de raíz. Los nodos mantienen entre ellos una relación que define una estructura jerárquica de “paternidad” entre ellos.
Recursivamente: un árbol puede verse como una estructura formada por la raíz de dicho árbol y una lista de árboles (los hijos).
Este nodo raíz es el padre de las raíces de los árboles que componen la lista, a partir del cual, se establece la relación de paternidad entre ellos. El conjunto vacío de nodos es un árbol, llamado nulo o vacío
Caracteristicas
Formas De Recorrer Un Arbol
Hay tres maneras de recorrer un árbol:preorden, inorden y posorden
Preorden
Recorrer un árbol en preorden consiste en examinar el dato del nodo raíz, posteriormenete se recorre el subárbol izquierdo y finalmenete se recorre el subárbol derecho (R.I.D)Inorden
Recorrer un árbol en inorden consiste en en recorrer el subárbol izquierdo, luego se examina el dato del nodo raíz y finalmente se recorre el subárbol derecho (I.R.D)Posorden
Recorrer un árbol en poorden consiste primero en recorrer el subárbol izquierdo, luego se recorre el subárbol derecho y por ultimo el nodo raíz (I.D.R)Arboles Binarios
En un árbol binario cada nodo puede tener como máximo dos subárboles tanto en el subárbol izquierdo como en el subárbol derecho
Arboles Binarios Similares
Dos árboles binarios son similares cuadno sus estructuras son idénticas, pero la información que contienen sus nodos diferentes
Arboles Binarios Equivalentes
Los árboles binarios equivalentes se definen como aquellos que son similares y además los nodos contienen la misma informacion
Arboles Tejidos
Los árboles tejidos son los que tienen apuntadores llamados hebras que apuntan a sus sucesores y los sucesores apuntan apuntan a los antecesores.
Tejer un árbol es hallar los apuntadores que hacen falta en su recorrido
Caracteristicas
- Nos permite disminuir el número de apuntadores a NUll
- Es mas ágil en el recorrido
- No se necesita la pila
- En un árbol de n nodos existen:
- (n-1) Apuntadores a nodos
- (n+1) Apuntadores a Null
- 2n Apuntadores
- Existen 3 clases de tejidos
- Tejido a la izquierda
- Tejido a la derecha
- Tejido Completo
Arboles AVL
Un árbol AVL (llamado así por las iniciales de sus inventores: Adelson-Velskii y Landis) es un árbol binario de búsqueda en el que para cada nodo, las alturas de sus subárboles izquierdo y derecho no difieren en más de 1.
No se trata de árboles perfectamente equilibrados, pero sí son lo suficientemente equilibrados como para que su comportamiento sea lo bastante bueno como para usarlos donde los ABB no garantizan tiempos de búsqueda óptimos.
Cuando el árbol se encuentra desequilibrado lo que se busca es equilibrarlo para ello se manejan las rotaciones como las siguientes
Rotacion Simple Por La Derecha
Se implementa cuando el factor de balance de la derecha sea 2 y cuando, la raíz del subárbol izquierdo tenga un factor de balance de 1, es decir, que esté cargado a la izquierda
Rotacion Simple Por La Izquierda
Este es lo contrario de la rotacion simple por la derecha, cuando su factor de balance por la izquierda sea 2 y cuando, la raíz del subárbol izquierdo tenga un factor de balance de 1, es decir, que esté cargado a la derecha
Doble Rotacion Por La Derecha
Se hace una simple rotacion por la izquierda y luego se hace una simple rotacion por la derecha
Doble Rotacion Por La Izquierda
Se hace una simple rotacion por la derecha y luego se hace una simple rotacion por la izquierda
Arboles B
Los árboles B árboles son estructuras de datos de árbol que se encuentran comúnmente en las implementaciones de bases de datos y sistemas de archivos. Son árboles binarios de búsqueda en los cuales cada nodo puede poseer más de dos hijos.
La idea tras los árboles-B es que los nodos internos deben tener un número variable de nodos hijo dentro de un rango predefinido. Cuando se inserta o se elimina un dato de la estructura, la cantidad de nodos hijo varía dentro de un nodo. Para que siga manteniéndose el número de nodos dentro del rango predefinido, los nodos internos se juntan o se parten.
Caracteristicas
- Se utilizan para manejar archivos que contienen gran caridad de información
- Se utilizan como método de búsqueda externa
- Fueron propuestos por Bayer Mccreight en 1970
- Cada nodo (pagina) en un árbol B de orden N contiene 2N claves como máximo y N claves como mínimo
- Cada pagina tiene 2 hijos como máximo y N+1 hijos como mínimo excepto la pagina raíz que puede tener como mínimo 1 clave y por consiguiente 2 hijos
- Las paginas se almacenan en dispositivos secundarios y la pagina raíz se almacena en memoria principal.
- Las paginas hojas están todas al mismo nivel
Operaciones en el árbol B
Arboles B+
Los arboles B+ son una variante de los arboles B, se diferencian en que los arboles B+ toda la información se encuentra almacenada en las hojas . En la raíz y en las paginas internas se encuentran almacenado indices o claves para llegar a un dato
Caracteristicas
- La raíz almacena como mínimo un dato y como máximo m-1 datos
- La pagina raíz tiene como mínimo dos descendientes
- Las paginas intermedias tienen como mínimo (m-1)/2(Parte entera) datos
- Las paginas intermedias tienen como máximo m-1 datos
- Todas las paginas hojas tienen la misma altura
- Toda la información se encuentra almacenada en las paginas hoja, por lo que en las paginas internas se puede duplicar la claves
- La información se encuentra ordenada
Aqui podremos observar un ejemplo
GRAFOS
¿Que son los grafos?
Es un conjunto de nodos o vértices conectados por arcos o aristasCaracteristicas
- Es una rama de las matemáticas y de la computacion
- Son estructuras de datos que permiten relacionar objetos(puntos)
- Estan compuestos por nodos(vertices) y aristas(lazos)
- Se utilizan en el manejo de redes, En la construccion de circuitos, en estrategia de ventas, economia, cartografia, topografia
Tipos de grafos
Grafo dirigido(Digrafo)
Componentes conectados separadamente
Grafo o Digrafo fuertemenete conectado
Grafos o Digrafos debilmente conectados
Camino simple
Grafo Euleriano
Grafo Hamiltoniano
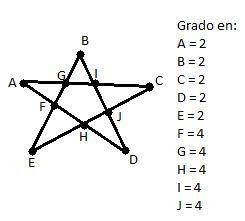
Grado de un vertice
Grafos regulares
Multigrafo
Estructura donde dos vertices estan unidos por más de un arcoGrafo simple
Grafo Completo
Grafo simetrico
Sus arcos tienen una sola direccion
Adyacencia
Existe adyacencia entre dos vertices si estan unidos por una arista
Incidencia
Los arcos inciden en los vertices si una de sus puntas llega a ese vertice
Si desde cualquier vertice podemos llegar a los demas
Si por lo menos desde un vertice no puedo llegar a los demas
Si partiendo de cualquier vertice podemos recorrer la estructura sin repetir vertices ni arcos
Si partiendo de cualquier vertice podemos recorrer todos los arcos llegando de nuevo al vertice origen se puede repetir los vertices cuantas veces sea necesario, los arcos se pueden recorrer solamente una vez
Si partiendo de cualquier vertice podemos recorrer todos los vertices sin repetir ninguno y finalmente llegar al vertice origen. Los arcos se pueden repetir
Orden de un grafo
Es el número de vertices que posee el grado
Es el numero de arcos que inciden en ese vetice
Es regular si todos los vertices tienen el mismo grado
Es aquel que no tiene arcos ciclicos
Si cada vertice tiene un grado igual a n-1 donde n es el número de vertices del grado
Si al doblar la matriz por la diagonal mayor coinciden los ceros y los unos
Lista de Adyacencia
Cada vertice se asocia a los vertices que apunta(adyacentes)
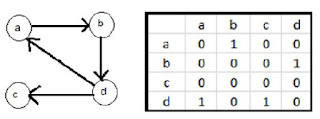
Matriz de Adyacencia
En la matriz de adyacencia se pone 1 a los vertices adyacentes y 0 a los que no tengan adyacencia
- Para determinar cuando utilizamos una lista o una matriz, se observa si el grado es disperso o no
Lista de Adyacencia Invertida
Almacena para cada vertice la lista de adjuntos desde otros vertices
Con la estructura se puede calcular el grado de entrada de cualquier vertice solamente contando el número de nodos de la lista del vertice requerido
Digrafo Fuertemenete Conectado
Un digrafo esta fuertemenete conectado si desde cualquier vetice podemos llegar a todos los demas
Es necesario hallar la matriz de caminos y si en la matriz obtenemos camnos diferentes a 0 es fuertemente conectado
Algoritmo de Warshall
Objetivo
Encontrar la clausura transitiva de un grafo por medio de las matrices de adyacencia. Esto mejoraría el método de la matriz de caminosCaracterísticas del Algoritmo de Warshall
- Es un ejemplo de algoritmo booleano
- Se obtiene una mtriz de adyacencia
- Se halla una matriz transitiva(cierre transitivo)
- El grafo tiene que ser dirigido
¿Que es una matriz transitiva o cierre transitivo?
La clausura transitiva o cierre transitivo de una relación binaria es encontrar la relación binaria mas pequeña, que siendo esta transitiva contiene al conjunto de pares de la relación binaria original.Conociendo ya que es una clausura transitiva vamos a hacer un ejemplo paso a paso
EJEMPLO
Se tiene un grafo dirigido de cuatro nodos y se hace una matriz de adyacencia(matriz de caminos)
- Lo siguiente es tomar uno de los nodos, podemos tomar el que queramos
- Cuando se toma como referencia es como si el nodo que eleimos ya no estuviera
- Volvemos realizar la matriz de adyacencia
- Los unos que ya obtuvimos en las matrices anteriores se mantienen
- Tendremos que hacer este proceso segun la cantidad de nodos que se tengan
- Ahora tomamos como base el nodo b y hallamos M2
- Tomamos como base el nodo d y hallamos M3
- Por ultimo tomamos como base el nodo c y hacemos M4
- Como nos podemos dar cuenta el nodo c no esta apuntando hacia ningún otro nodo por lo tanto la M4 quedara igual a la M3
- M4 es la es la que nos va a permitir ver todos los posibles caminos que hay en el grafo
- a esta ultima matriz es a la que se le conoce como matriz de clasura transitiva
APLICACIONES DE GRAFOS
¿Que es un grafo?
Un grafo es una representacion gráfica de diversos puntos que se conocen como nodos o vértices, los cuales se encuentran unidos a través de líneas que reciben el nombre de aristas¿Que es un vértice o nodo?
Un vértice es la unidad fundamental de la que están formados los grafos
¿Que es una arista o arco?
Conecta dos vértices. Una arista dirigida es una arista de un dígrafo y tiene una dirección asociada consigo, esto es, posee un vértice inicial y un vértice final. Una arista no dirigida es una donde no se distingue un vértice inicial ni uno final.
¿Que es adyacencia?
Dos vértices son adyacentes si el grafo contiene al menos una arista que los une.
¿Que es un bucle o lazo?
Un bucle o lazo en un grafo es una arista que conecta al mismo vértice consigo mismo. Un grafo simple no puede tener bucles.
¿Que es un camino?
Un camino es una sucesión de vértices tal que de cada uno de sus vértices existe una arista hacia el vértice sucesor¿Que podemos representar en un grafo?
- Red de computadores
- Conexiones de vuelo de una aerolínea
- Carreteras que unen ciudades
- Circuitos electricos
- Representacion de paradas de autobús
ALGORITMO DE DIJKSTRA
¿Como funciona?
- Inicializar todas las distancias en D con un valor infinito relativo ya que son desconocidas al principio, exceptuando la de x que se debe colocar en 0 debido a que la distancia de x a x sería 0.
- Sea a = x (tomamos a como nodo actual).
- Recorremos todos los nodos adyacentes de a, excepto los nodos marcados, llamaremos a estos nodos no marcados vi.
- Para el nodo actual, calculamos la distancia tentativa desde dicho nodo a sus vecinos con la siguiente fórmula: dt(vi) = Da + d(a,vi). Si la distancia tentativa es menor que la distancia almacenada en el vector, actualizamos el vector con esta distancia tentativa. Es decir: Si dt(vi) < Dvi → Dvi = dt(vi)
- Marcamos como completo el nodo a.
- Tomamos como próximo nodo actual el de menor valor en D (puede hacerse almacenando los valores en una cola de prioridad) y volvemos al paso 3 mientras existan nodos no marcados.
Caracteristicas
- Es un algoritmo Greddy.
- Trabaja por etapas, y toma en cada etapa la mejor solución sin considerar consecuencias futuras.
- El óptimo encontrado en una etapa puede modificarse posteriormente si surge una solución mejor.
Consideraciones
- Si los pesos de mis aristas son de valor 1, entonces bastará con usar el algoritmo de BFS.
- Si los pesos de mis aristas son negativos no puedo usar el algoritmo de Dijsktra.
ALGORITMO DE KRUSKAL
Historia
Joseph B. Kruskal , en 1956 descubrió este algoritmo para la resolución del problema Árbol de coste total mínimo (mínimum spinning tree - MST) también llamado árbol recubridor euclídeo mínimo.Este es un problema típico de optimización combinatoria, que fue considerado originalmente por Otakar Boruvka (1926) mientras estudiaba la necesidad de electrificación rural en el sur de Moravia en Checoslovaquia.
Introduccion
El algoritmo de Kruskal es un algoritmo de la teoría de grafos que se usa para encontrar un árbol recubridor en un grafo conexo y poderado
Es decir busca un sobconjunto de aristas que, formando un árbol, incluyen todos los vértices y donde el valor total de todas las aristas del árbol es el mínimo.
Aplicaciones
La aplicación típica de este problema es el diseño de redes telefónicas. Una empresa con diferentes oficinas, trata de trazar líneas de teléfono para conectarlas unas con otras. La compañía telefónica le ofrece esta interconexión, pero ofrece tarifas diferentes o costes por conectar cada par de oficinas. Cómo conectar entonces las oficinas al mínimo coste total.
La formulación del algoritmo también ha sido aplicada para hallar soluciones en diversas áreas (diseño de redes de transporte, diseño de redes de telecomunicaciones - TV por cable, sistemas distribuidos, interpretación de datos climatológicos, visión artificial - análisis de imágenes - extracción de rasgos de parentesco, plegamiento de proteínas, reconocimiento de células cancerosas, y otros).
Ejemplos
Teoria en la vida real
GRAFOS PARTICULARES
Grafo nulo
En este grafo los vértices que lo componen no estan conectados, esto es, que son vértices aislados, se puede decir también, que es un grafo trivial que no tiene vértices ni aristas.
Grafo Vacío
Es aquel grafo que no tiene aristasGrafo trivial
Es un grafo trivial es un grafo con 0 aristas, y 0 ó 1 vértices. Los grafo triviales son grafos completos: a aquel que no posee vértices se le llama grafo nulo, mientras que al que posee un vértice, se le conoce como grafo singleton.Grafo simple
Es aquel grafo que no posee bucles o lazos
Grafo completo
Un grafo completo es un grafo simple en el que cada par de vértices están unidos por una arista, es decir, contiene todas las posibles aristas. Se puede hacer referencia que un grafo completo de n vértices tiene n(n-1)/2 aristas, y se nota Kn. Es un grafo regular con todos sus vértices de grado n-1. La única forma de hacer que un grafo completo se torne disconexo a través de la eliminación de vértices, sería eliminándolos todos.
Grafo bipartito
Es aquel grafo bipartito en el que todos los vértices de la particion V1 están conectados a todos los vértices de la partición V2 y viceversa
Grafo rueda
Es un grafo con n vértices que se forma conectando un único vértice a todos los vértices de un ciclo-(n-1). Se puede decir también, que un grafo rueda (Wn), o simplemente rueda, es un grafo con n vértices que se forma conectando un único vértice a todos los vértices de un ciclo-(n-1).
Grafo plano
Es aquel que puede ser dibujado en el plano cartesiano sin cruce de aristas.Grafo perfecto
Es aquel que el número cromático de cada subgrafo inducido es igual al tamaño del mayor clique de ese subgrafo
Aplicacion de la Teoria de grafos Grafos bipartitos Grafos completos de N vértices
ARBOLES ENEARIOS
Un árbol n-ario puede tomarse como un árbol de n elementos con arboles de n elementos asociados a cada uno de sus componentes.
Se pueden encontrar tres clases de recorridos para este tipo de árboles: pre-orden, in-orden y pos-orden.
Posee los mismos conceptos que un árbol binario: nodos, raíz hoja, camino, rama altura y peso.
Las tres operaciones que se pueden llevar a cabo sobre este tipo de arboles son sustracción, adición y búsqueda.
Existen algoritmos para cada uno de estos procedimientos, de la manera que se presenta a continuación
Algoritmo
Es muy similar a la de un árbol
Primer nivel
- Trata el caso de un árbol vacío
- Crea estructuras de datos como iteradores
Segundo nivel
- Planteamiento recursivo
- Se tienen n avances posibles en la recursión
- Se requiere un ciclo para iterar sobre cada avance
Usos
Árbol de busqueda binaria
Que se Utiliza en muchas aplicaciones de búsqueda donde los datos es constantemente entrada/salida, tales como el map y set objetos en muchos idiomas, bibliotecas.
Binary Space partition
Que se Utiliza en casi todos los de vídeo 3D juego para determinar qué objetos deben ser prestados.
Binario trata
Se Utiliza en casi todos los de alto ancho de banda del router para almacenar router-tablas.
Hash Árboles
Se usa en los programas p2p y especializado imagen de la firma en la que un hash debe ser verificado, pero todo el archivo no está disponible.
Matrices dispersas
¿Que es una matriz dispersa?
La matriz dispersa contiene formatos de almacenamiento en memoria, el objetivo es poder utilizar menos memoria de la que normalmente consume un equipo para el procesamiento de información.
¿Como inicio?
Inicialmente fue utilizada en la computación científica, especialmente en la optimización a gran escala de análisis estructural y de circuitos.
Igualmente fue aplicada en la teoría de grafos, teoría de redes, métodos.
Siempre buscando el mejor método para el menor consumo de memoria.
Tipos de formato
Los formatos que se representaran a continuación, mostraran las diferentes formas de como han tratado de implementar este tipo de matrices en equipos de computo.
Lista enlazada
Es una estructura matriz donde se almacenan ceros (NULL) y unos (1), y la idea es crear una lista a partir de los elementos no vacíos. Ejemplo:
Como podemos ver en el nodo 1 se tiene el valor numérico 1, que se encuentra en la posición 1,4.
Formato coordenado
El formato coordenado es un avance frente a la lista enlazada ya que este tipo de formato se manejan con tres arreglos y el procesamiento de información es mejor.
Donde v = datos no nulos, i= fila donde se encuentra el dato y v= columna donde se encuentra el dato.
Lista enlazada por fila
Es mas eficiente que el formato coordenado y lo mejor es que este no tiene mayor uso de memoria.
Estos se reagrupan por fila por lo tanto, se tendrá una lista enlazada por cada fila matriz.
Fommato comprimido por filas
Conocido como CSR(Compressed Sparse Row), mas que todo utilizado en aplicaciones practicas, manejan los mismos tres vectores pero con una única diferencia:
El vector i almacenara la posición en donde empieza una nueva fila en el vector j.
Formato comprimido por columnas
Conocido como CSC(Compressed Sparse Column), manejan los mismos tres vectores pero con una única diferencia:
El vector j almacenara la posición en donde empieza una nueva columna en el vector i.
Ejemplos de matrices dispersas
http://www.redalyc.org/articulo.oa?id=84927487025
https://www.youtube.com/watch?v=kzJ9Ux2xwSI